Las Paradojas de Zenón

Hoy desperté con ganas de aprender un poco más sobre filosofía. Claro, digo hoy, pero en realidad estoy en lo mismo toda la semana. Mi racionamiento (¿no es eso lo que hacen los filósofos?) es que si hay que aprender sobre filosofía, no basta con leer los autores modernos populares (como Sartre, Unamuno o Nietzsche). Hay que empezar estudiando la filosofía antigua. Hay que empezar con los griegos.

Así llegué a los filósofos eleáticos, del período conocido como presocrático. Tal vez el filósofo más conocido de esa escuela fue Parménides que enseñaba, básicamente, sobre el ser (El Ser Es). Uno de sus discípulos, el más conocido, fue Zenón.

Este último defendió las teorías de su maestro, a quien acompañó en varios discursos (a los cuales, se dice, asistía Sócrates. Sin embargo, su fama viene de varias paradojas que formuló. Las que me interesan en este momento son cuatro que argumentan en contra del movimiento. En realidad, no quiero que me malinterpreten, los escritos de los filósofos de esa época son pocos y están incompletos. Es improbable (por motivos lógicos) que Zenón haya tratado de desmentir el movimiento. Lo más seguro es que, simplemente, quería decirnos que es muy difícil explicarlo o demostrarlo. A continuación, las paradojas de Zenón contra el movimiento, en mis palabras:

1. La dicotomía: Un hombre lanza una piedra hacia un objetivo determinado. Antes que la piedra llegue al final, debe recorrer la mitad del camino. Desde ahí, debe recorrer, de nuevo, la mitad del camino antes de llegar a su objetivo. Una vez más, entonces, debe recorrer otra mitad, y así sucesivamente hasta el infinito. Por tanto, la conclusión de Zenón es que si la piedra debe recorrer intervalos infinitos, nunca llega a su destino.


2. Aquiles y la tortuga: Aquiles es el hombre más rápido del mundo antiguo. Un buen día decide correr contra una tortuga, 10 veces más lenta que él. Aquiles decide, entonces, darle una ventaja de, digamos, diez metros. Entonces, cuando el corredor avanza los diez primeros metros, la tortuga avanzó uno. Aquiles avanza ese metro, la tortuga le lleva le delantera por un decímetro (10 centímetros). Así, igual que el caso anterior, hasta el infinito. Por eso, Aquiles nunca puede ganarle a la tortuga.

3. La flecha: El arquero lanza una flecha. Esta flecha, ¿está en movimiento? Analicemos como lo hizo Zenón. En un instante dado, la flecha ocupa un espacio exactamente igual a ella misma. Por tanto, en ese instante, tenemos una flecha estática. En el momento siguiente, lo mismo. Así, nos damos cuenta que el “movimiento” en una suma de momentos en que no existe ese movimiento. Por tanto, el movimiento tal no existe.



4. El Estadio: Primero, el reconocimiento. Yo no entiendo esta paradoja. Pero aquí vamos a explicarla igual. En un estadio hay tres filas con hombres de cuerpos del mismo tamaño.


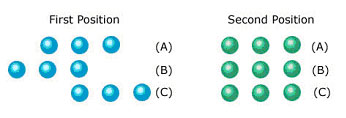
En el gráfico vemos como están organizadas las filas y como se mueven. AAA están estáticos. BBB se mueven hacia la derecha, mientras que CCC hacia la izquierda. El movimiento de ambas filas se realiza a la misma velocidad. El primer hombre B recorre un espacio igual a dos A, pero, en el mismo tiempo, el primer C recorre cuatro hombres B. Dado que los tamaños de A, B y C son iguales, se concluye que la velocidad de los C es doble que la de los B. Sin embargo, ya habíamos dicho que la velocidad era la misma.

No se trata de buscar soluciones a estas paradojas. Existen, para todas ellas. Pero es interesante plantearse el movimiento así, y tratar de explicarlo. Zenón plantea estas paradojas tal vez como un ejercicio mental. Bajo los supuestos de ellas, no tienen solución. Para resolverlas, entonces, hay que mirar hacia fuera. Creo que es un buen consejo.